この記事を書いた人
- 村上 仁セールス＆マーケティンググループ/マーケティングディレクター（ビジネス・アーキテクツ）
出版業界の編集者からWeb業界のディレイター・マーケターに転身。大手ポータルサイトのコンテンツ制作や海外SaaSツールのプロジェクトマネージャー等を経験。ビジネス成果にこだわったマーケティング戦略の立案およびサイト制作、データ分析が強み。
本記事では、データ分析を担当している企業のマーケターやWeb担当者向けにデータリテラシーを高める実践的ナレッジをご紹介いたします。
今回は、データを扱う上で最も大切かつ基礎となる「平均値」について、土台となる知識をおさらいしつつ、実務に役立つ応用法まで具体例を交えながら解説していきます。少 しクセのある指標だけにしっかりと押さえてください。
取り扱い注意！ダマされないための「平均値」のトリセツ
日常的に慣れ親しんだ「平均値」ですが、その特性や使い方をしっかり把握していますか？まずは、データ分析の基礎中の基礎とも言える「平均値」について、改めておさらいしながら、実務で生かせる活用法をご紹介します。
ビジネスパーソンなら押さえておきたい「3つの平均値」
データ分析の際に誰もが扱う「平均値」。小学生で習うこの数字には、いろいろな種類があることをご存じでしょうか？
一般的な算術平均のほか、ビジネスパーソンならぜひ押さえておきたい3つの平均値をまとめました。
- 算術平均（相加平均）
- 加重平均
- 幾何平均（相乗平均）
算術平均（相加平均）
全データの和をデータの個数で割った値。「平均」といえばだいたいこのことを指します。
加重平均
基本は算術平均と同じですが、各データの重要度に応じた重み付けをした計算方法。
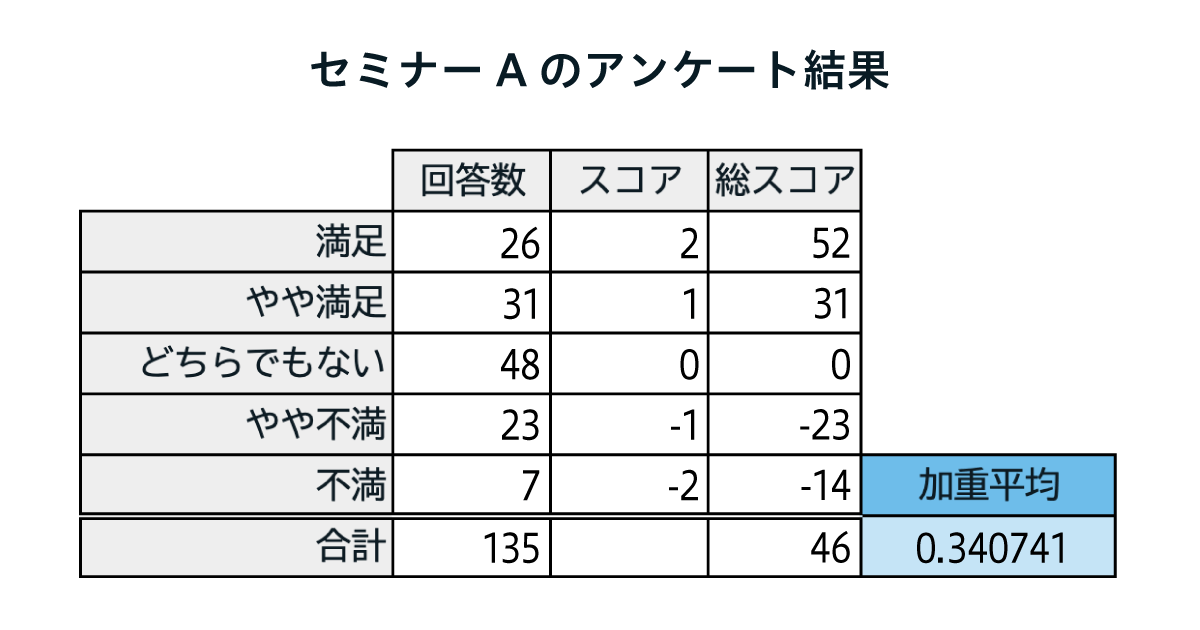
例えば、セミナーの満足度をアンケート結果から導き出す方法として、各満足度に対して「スコア」を割り振り、「回答数」×「スコア」＝「総スコア」を算出します。「総スコア」の合計を「回答数」の合計で割った値が加重平均です。
下図（図1）の場合、加重平均は0.34となります。セミナーの満足度としては「どちらでもない」よりは良かったけれども「やや満足」までは届かなかった、という評価を表すことができます。このように、数値化しづらいデータも定量的に評価することが可能になります。
図1：加重平均の表
幾何平均（相乗平均）
複利計算をベースとした、比率や割合で変化する数値に対してその平均を求める計算方法。企業の成長度合いを測る指標として計算されるCAGR（年平均成長率）などが有名です。
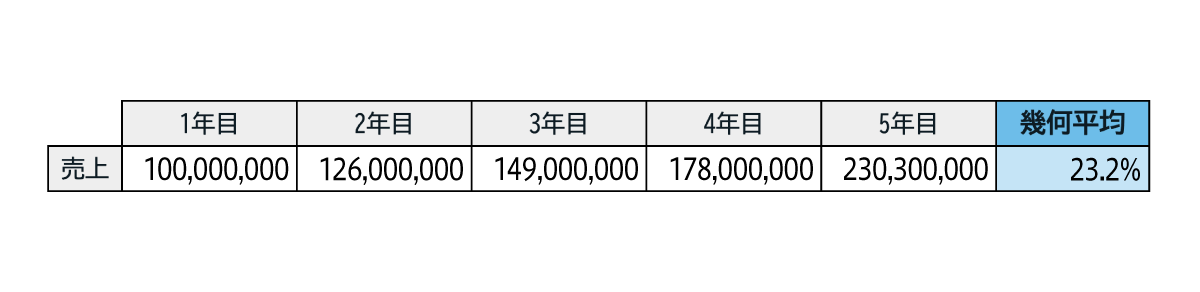
下図（図2）は、5年間の売上が1億円から2.3億円に増えた場合の例です。年平均成長率を求めると、約23.2％ずつ成長していると言えます。
計算式はやや複雑ですが、Excelで計算すると以下のような式になります。
- CAGR＝(G3/C3)^(1/(5-1))-1
図2：幾何平均の表
母校OBの平均年収を4,000万円UPさせた「大谷マジック」
2023年12月、SNSやインターネットが「花巻東高校OBの平均年収が4,000万円増加した」という話題で盛り上がったのをご存じでしょうか？
大谷翔平選手が、ロサンゼルス・ドジャースと10年で総額約1,015億円という、当時史上最高額の契約をしたニュースが世界中で話題になりました。大谷選手の影響力の大きさを物語る話としてとても興味深いですね。
ですが、これをもって花巻東高校OBの平均年収が本当に4,000万円上がったと信じる人はいませんよね。
つまり、大谷選手という明らかに大きな「外れ値」が花巻東高校OBたちの平均年収に影響を与えたのです。これも「大谷マジック」の1つなのでしょうか？こうした「外れ値」による平均値への影響は、値が大きかったりデータ量が少なかったりするほど、その影響度合いが大きくなります。
では、もう1つ身近な調査データを見てみましょう。厚生労働省が毎年発表している日本の平均所得を表した統計データです。下図（図3）は、「2023（令和5）年 国民生活基礎調査」にて発表された2023年（令和5年）度の調査データから引用した図です。
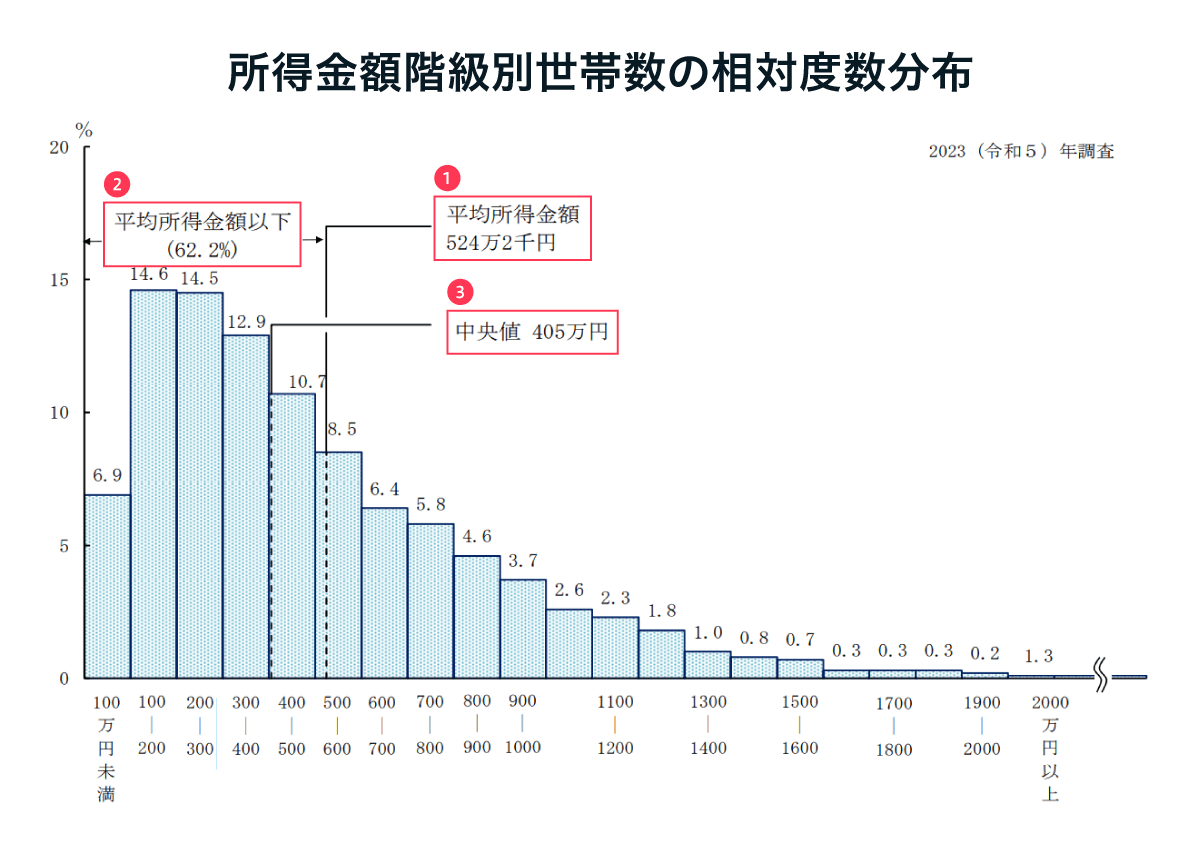
図3：所得金額階級別世帯数の相対度数分布（2023年度調査）
引用 : 厚生労働省. 2023（令和５）年 国民生活基礎調査の概況（PDF）.2023（令和５）年. (参照 2025-03-11)
このデータを見ると、「平均所得金額（赤枠①）」は524万2,000円となっています。この調査結果が公表される度に、自分の年収はこの平均値よりも高いか低いか気になってしまうという方もいるのではないでしょうか。
さらにこのグラフをよく見てみると、「平均所得以下（赤枠②）」の割合はなんと62.2％にも上ります。過半数以上の人がこの平均所得以下ということが示されていますが、はたして赤枠①の「平均所得金額」は、データ全体を表現する指標としてふさわしいでしょうか？どこか違和感がありませんか？
こうした大きく偏りがあるデータを読み解く上で知っておきたいのが、グラフにも示されている「中央値（赤枠③）」と呼ばれる「代表値」の1つです。データ全体の特徴を把握するのに非常に有効な値ですので次の章で深掘りしていきます。
データ分析は「5つの代表値」の把握から
データ分析を行う際には、まず与えられたデータがどのような性質のデータなのかということを把握する必要があります。以下に列挙する「代表値」と呼ばれる5つの指標を算出することでデータの全体像がわかります。まずは、手元のデータでもこの指標をしっかりと把握することから始めてみてください。
最大値
データ内で最も大きな値。
この値を押さえておくことで、データに外れ値が含まれているかどうかを見極めるヒントになります。
最小値
データ内で最も小さな値。
最大値と同様に、データに外れ値が含まれているかどうかを見極めるヒントになります。
中央値
データの物理的な真ん中を示す値。
データを小さい順に並べた中央に当たる数値のこと。データが奇数個の場合は1つの値が中央値になりますが、データが偶数個ある場合は最後に残った2値の平均値を中央値とします。その特性からこの指標は外れ値の影響を受けにくいというメリットがあります。
平均値
算術平均（相加平均）です。
最頻値
データ内で最も多く出現した数値。
ここで、先ほどの図3を見てみると「中央値（赤枠③）」は405万円。平均値と中央値の間には、約119万円もの開きがあることがわかります。中央値は外れ値の影響を受けにくいですから、平均値よりも中央値の方がより実態を把握するのに適していると言えるのではないでしょうか。
このほかにも、同じようなことは私たちの周りでも見られます。
例えば、就職や転職活動などで企業の平均年収を調べてみると「1,000万円」と掲載されていたとします。しかし、図3や花巻東高校OBたちの平均年収のように、実態はごく一部の人がすごく稼いでいるだけで、全社員の中央値を見るともっと低いということもあり得ます。自社や応募企業の給与の中央値はいったいいくらなのか、気になりますよね。
さらに、マーケターやWeb担当者であればぜひ押さえておきたいのが、GA4の指標にある「平均セッション継続時間」や「セッションあたりの平均エンゲージメント時間」です。それぞれの計算式は、以下になります。
- 平均セッション継続時間
- 全セッションの滞在時間の合計 ÷ セッション数
- セッションあたりの平均エンゲージメント時間
- エンゲージメントの合計時間 ÷ セッション数
サイトのアクセス状況を把握するのには便利な指標ですが、これらの指標は当然「外れ値」も含まれた上で「平均」を算出していることがわかります。そうすると、この数値を見ることがユーザー像を正しく理解することにつながると言えるでしょうか？「もしかしたら中央値や最頻値の方が、ユーザーの実態にあっているのではないか？」そんな疑問が浮かんできませんか？
つまり、平均値は便利な半面、そのまま鵜呑みにすることが正しい理解の妨げになることもあります。本章で説明した5つの代表値と合わせてデータの中身をしっかりと見ることが大事なのです。今回ご説明した代表値は、データ全体の特徴を把握するのに非常に役立つ指標ですので、データ分析の際にはぜひ活用してみてください。
マーケティング・Web担当者必見！平均値の実践的活用法
ここまで読み進めると、なんだか平均値はあまり当てにならない数値だと思う方もいるかもしれませんが、もちろんそんなことはありません。
特にマーケターや企業のWeb担当者にとっては、扱い方1つでデータの見方が変わることもあります。
ここからは、これまで説明した「平均値」を具体的にWebデータでどのように活用するのか、その実践例をご紹介いたします。
【基礎編】「移動平均線」でサイトの傾向を把握する
「移動平均線」とは、一定期間のデータの平均値を折れ線グラフで表したものです。株取引をしている人にはおなじみで、株価や為替などのテクニカル分析によく用いられます。5日移動平均線や25日移動平均線など、株価のトレンドを把握する指標として活用している人は多いと思います。
同じように、Webサイトのアクセスデータでも移動平均線を用いることで、上昇トレンドなのか下降トレンドなのかといった傾向を把握するのに役立ちます。具体的にどのように活用するのか、Googleのデモアカウントの数値を元にExcelを使って解説します。
図4：Webサイトのアクセスデータ（2024年1月1日～2024年12月31日までのセッション数）
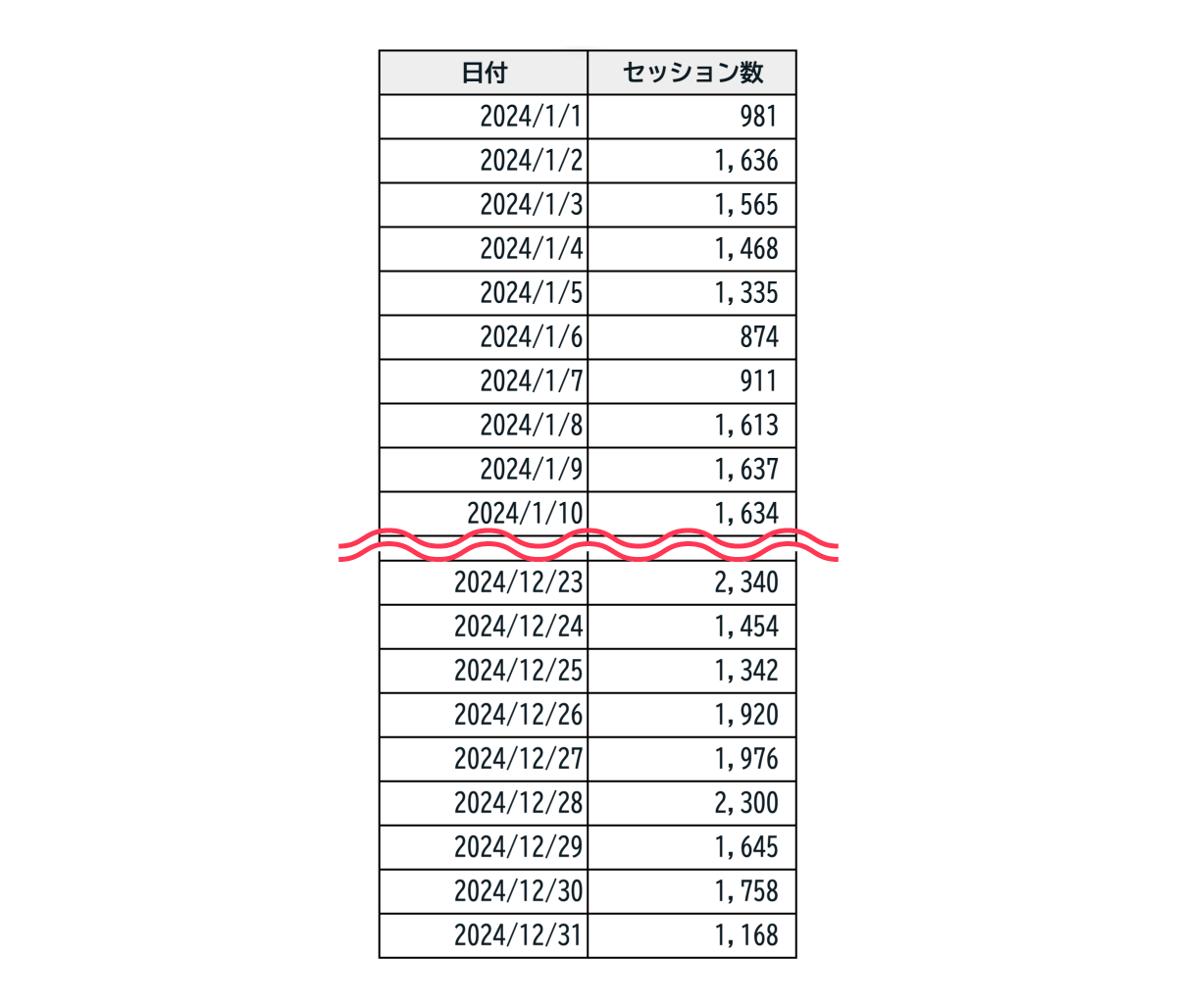
上記の図4のExcelデータ（2024年の1年間のセッション数）を元に、下の図5のグラフを作成しました。このデータを見て、サイトの状況を上司に報告しなければならない場合、どのように報告しますか？
「ポンッ、ポンッと跳ねているところがいくつかある一方で、年末あたりで落ち込んでいますが、だいたい3,000～4,000セッションの間で横ばいです。」
とパッと見て分かる情報を伝えているだけにとどまっていませんか？せっかくデータが取得できているので、より詳しい報告をするために、複数の視点から深堀りしたデータ分析を行いましょう。
図5：Webサイトのアクセスデータ（折れ線グラフ）
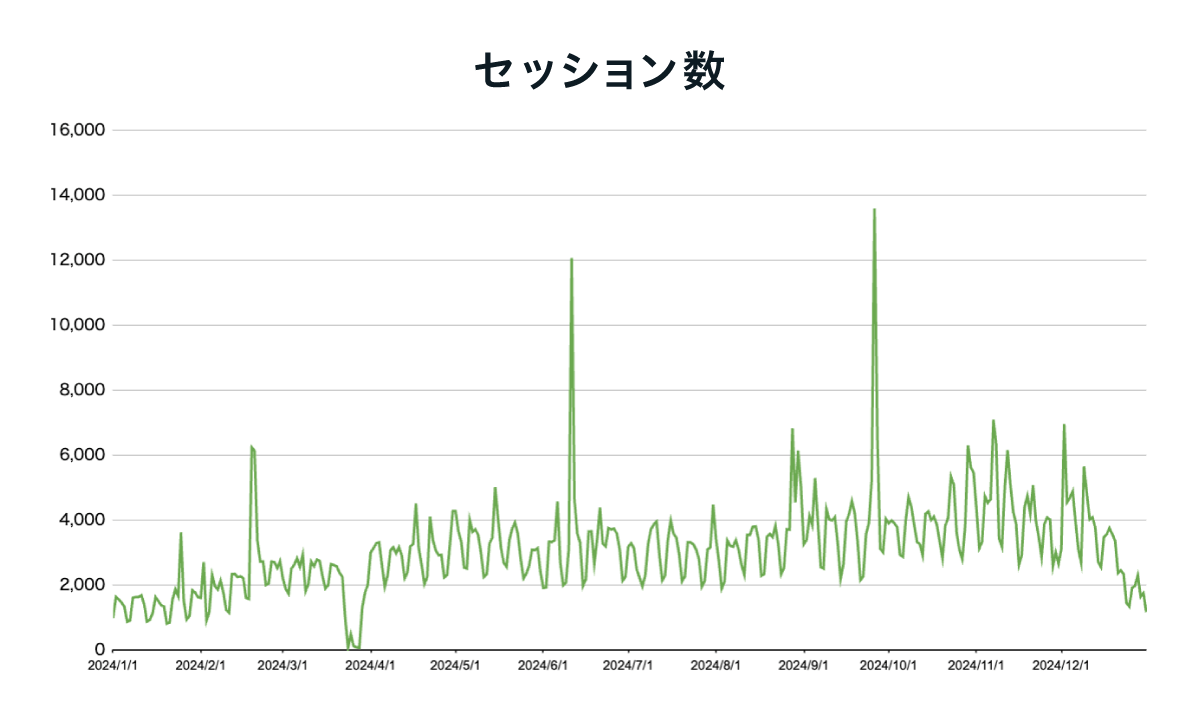
では、このグラフに30日移動平均線（図6、紫線）を追加してみるとどうでしょうか。
年始から緩やかな上昇トレンドにあったことがわかります。年末に向けての下降トレンドについては、季節性要因かどうか複数年のデータで比較してみないとわかりませんが、たった1本の移動平均線を引くだけでデータの解像度が上がったと感じませんか？
図6：Webサイトのアクセスデータ（30日移動平均線）
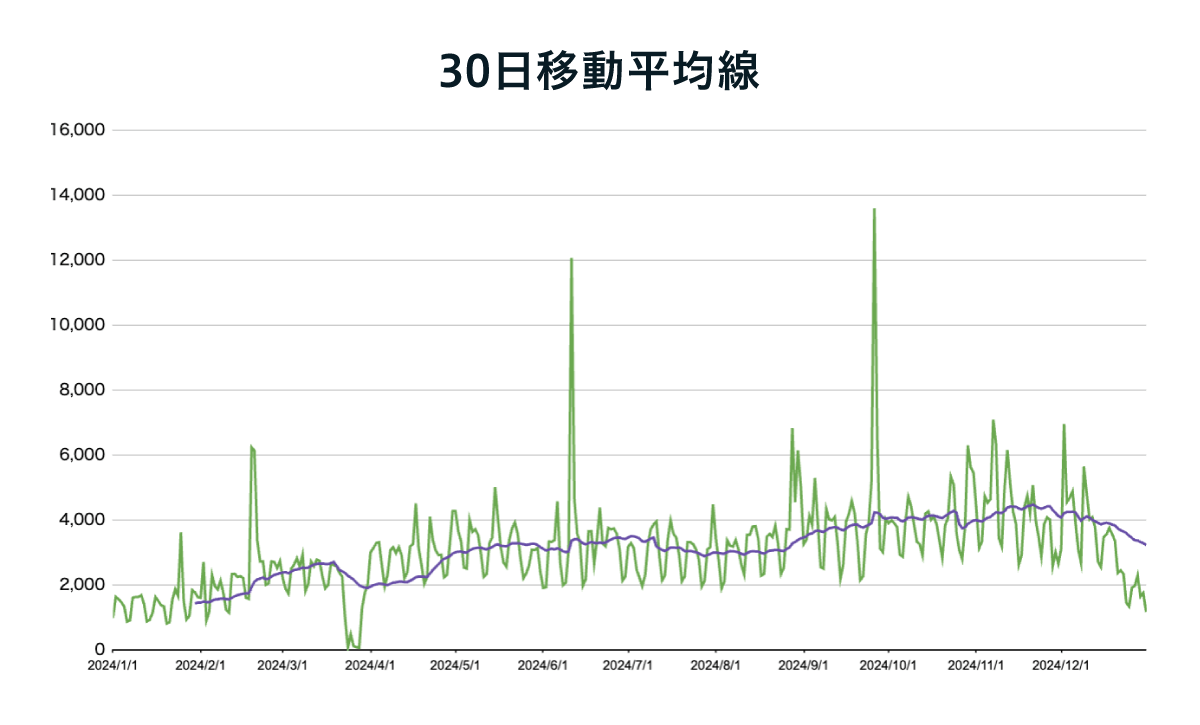
このようにデータから何かしら示唆を得る場合は、「何となく」や「だいたい」といった曖昧な言葉は排除する必要があります。それがひいてはデータドリブンな意志決定にもつながっていくのです。
ところで、図6の中で2月中旬、6月上旬、9月下旬に特に大きくグラフが跳ねている日があり、3月下旬には急落しているところがあるのが見て取れます。跳ねたところは何かキャンペーンを実施した効果なのか、急落したところはサーバーに何か障害が起こったのか原因はわかりませんが、明らかにほかの日とは異なる数値を記録しています。
UA（ユニバーサルアナリティクス）の時代であれば、ダッシュボードのグラフの下にメモ機能があり、いつどんな施策を打ったのかを追うことができましたが、GA4では残念ながら消えてしまいましたので、関係部署に確認するしかありません。
図6のような明らかに突出した数値は、誰もがパッと見ただけで「おかしくない？」と気づきますが、例えば9月1日辺りのグラフの突出具合は、どうでしょうか？異常だと言えますか？それとも「ちょっと跳ねただけ」だと思いますか？
これも、人によって受け止め方が異なるかもしれません。次の応用編では、こうした異常な値を検出するために、平均値を応用した検知方法を解説します。
【応用編】「標準偏差」で異常値を検知する
カップヌードルで有名な日清食品株式会社がどういう品質管理を行っているのかご存じでしょうか？
引用 : 工場での品質管理も見てみよう！. 原材料への取り組み｜カップヌードル｜CUPNOODLE. (参照 2025-03-06)
公式HPによれば「不良品発生率100万個に1個以下」という驚異的な安全基準を実現しているそうです。よく製造業の品質管理で見聞きするのが「シックスシグマ」という言葉です。これは、不良品を「100万個中、3.4個以内に納めよう」という考え方です。しかし、日清食品株式会社の安全管理は、それをはるかに上回る基準なのだとわかりますね。
こうした品質管理で用いられるたりするのが「標準偏差（シグマσ）」であり、先の「シックスシグマ（6σ）」も標準偏差を表しています。この標準偏差とは「データが平均値からどれだけばらついているのか」を表す指標です。
以下の図7で示す正規分布曲線は、±1σの間にはデータの約68.3％、±2σでは約95.5％、±3σでは約99.7％が含まれるという意味です。
図6のグラフに、正規分布曲線の標準偏差（シグマσ）を追加することで異常値の検出が可能になります。図8では±2シグマの範囲を、図9では±3シグマの範囲を水色の線で追加しています。図8、9に、それぞれの移動標準偏差（標準偏差を日ごとに算出しつなげた線）を水色の線でグラフに追加しています。水色の線から上下に突出している値を、異常値として赤丸をつけています。
図7：正規分布曲線
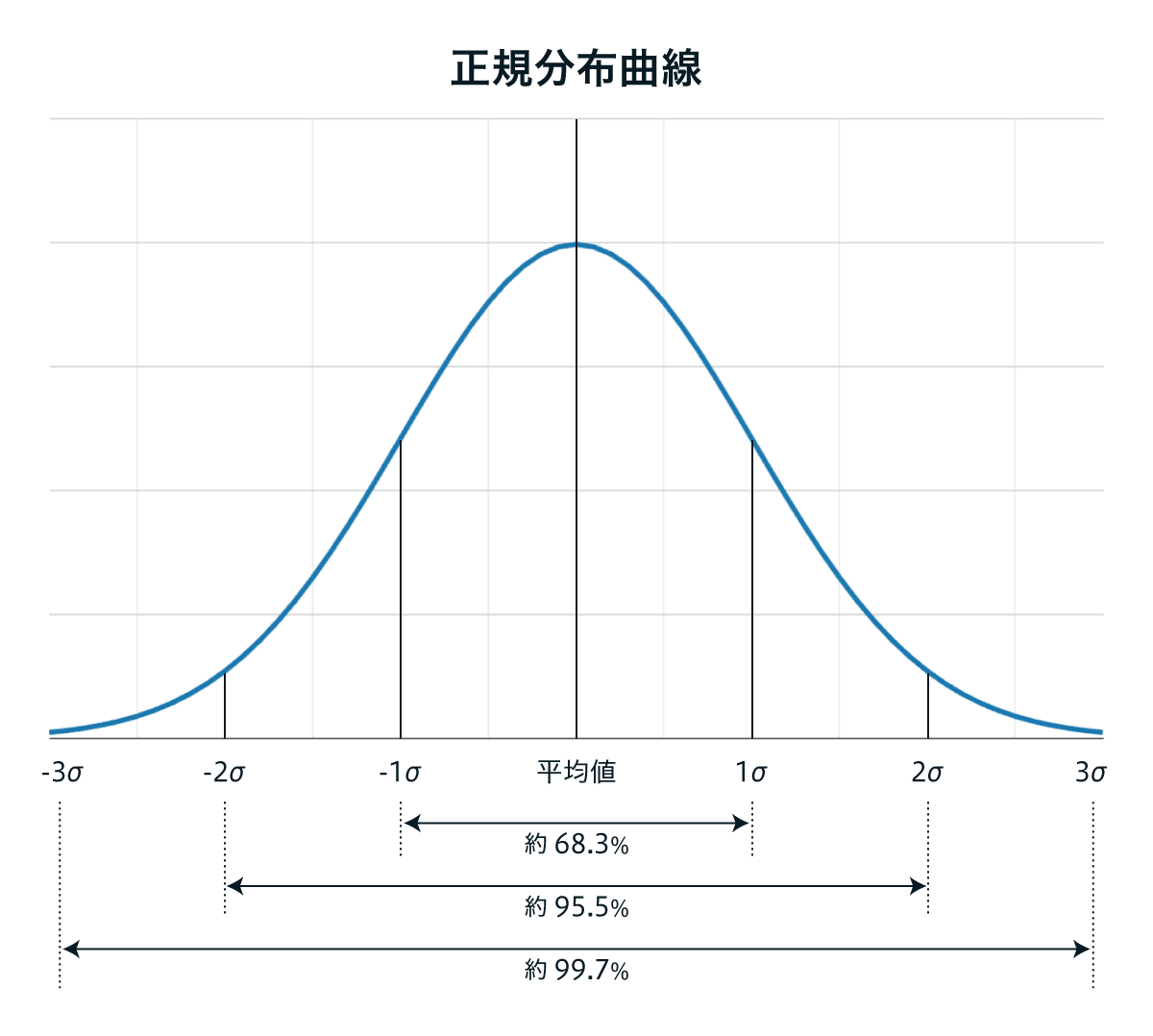
図8：移動標準偏差（±2シグマ）
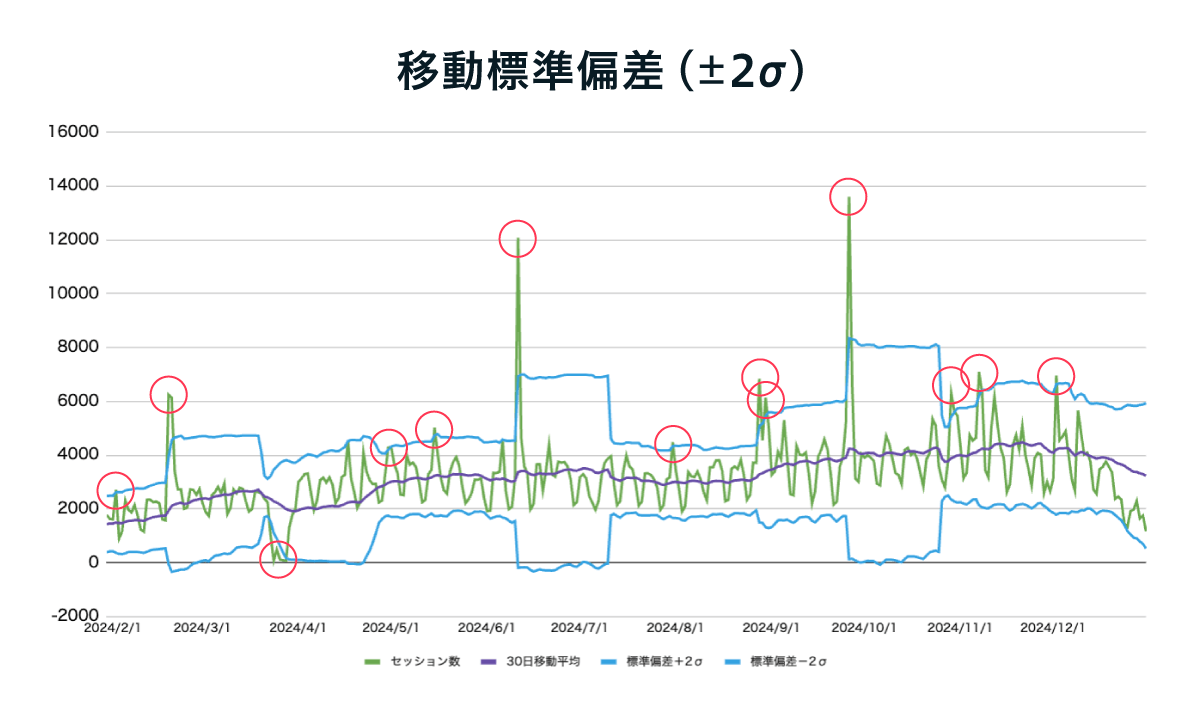
図9：移動標準偏差（±3シグマ）
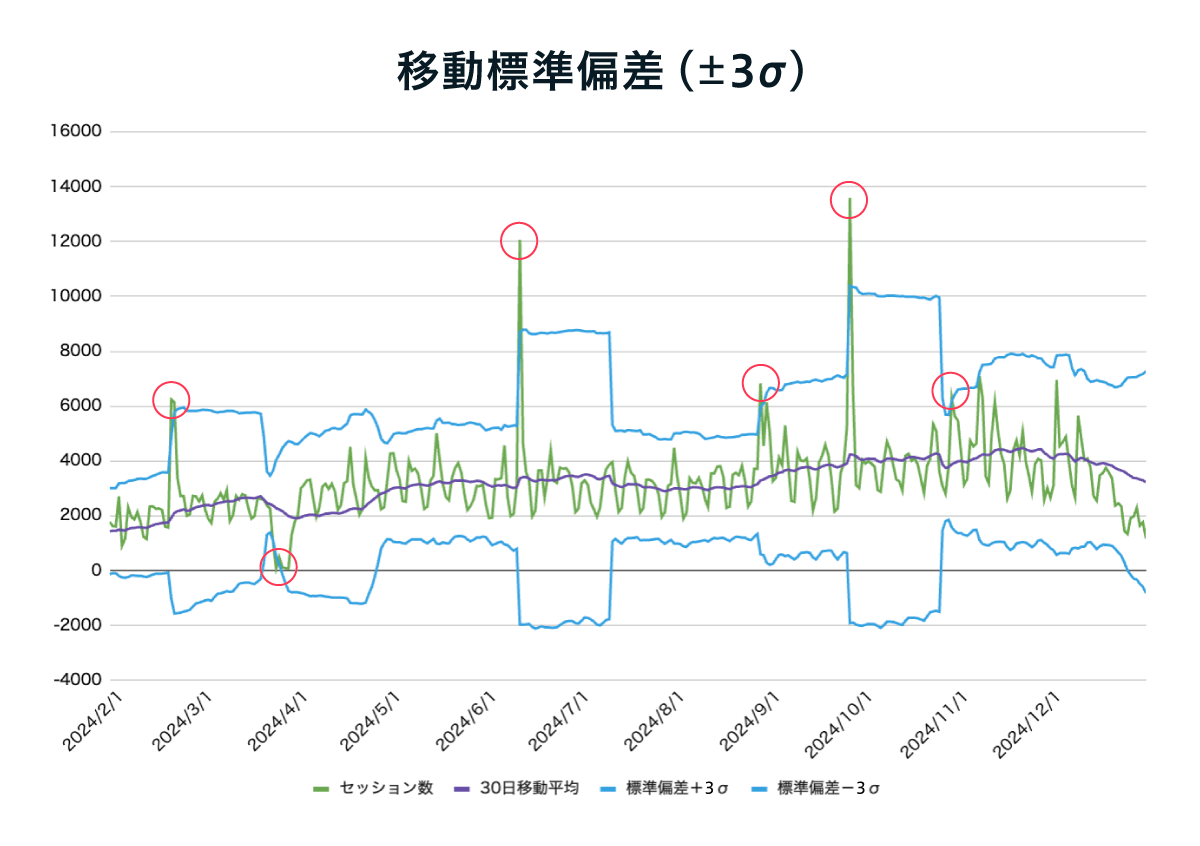
グラフの赤丸で囲った部分に注目すると、上下に描かれた水色の移動標準偏差の線から突出している箇所がわかります。
- ±2シグマ（図8）：13箇所
- ±3シグマ（図9）：6箇所
図7から±2シグマの線の内側には、約95.5％のデータが入っていますから、突出した約4.5％部分の一方は約2.25％の値ということになります。つまり突出した部分は「100回の内、2回しか起こらないような事象が起こっている」と読み解くことができます。
さらに±3シグマの場合は、線の内側には約99.7％のデータが入ることになりますから、突出した部分の事象が起こる確率は約0.15％です。つまり「1000回の内、1回しか起こらないような異常な事象が起こっている」と言えるのです。
異常値の判断基準を、±2シグマにするのか、あるいは±3シグマにするのかはビジネス判断になりますが、移動標準偏差のラインを越えた時の原因究明は必須です。特にキャンペーンなどの場合は、年に何度も行うことが一般的ですから、キャンペーンの勝ちパターンを見つける上でも大きなヒントになるでしょう。一方で、割り込んでしまった場合は大問題です。もしも、システム的な不具合であれば、影響が拡大しないように早急な対策が必要です。
まとめ：たかが平均値と侮るなかれ！
今回は、平均値をベースにしたデータ分析例をご紹介いたしました。たしかに取り扱いに注意が必要ですが、これまでGA4のセッションや表示回数などのグラフをサラッと流していた方も「こういう分析の仕方があるのか」とお気づきいただけたと思います。
BAsixsは、お客さまのビジネス課題を解決するために、ロジカルな戦略立案とデータドリブンなマーケティング施策をご提供しています。
どのようなご相談でも結構ですので、お気軽にお問い合わせください。お待ちしております。